Dear User,

Our previous post dealt with a Variational Principle – namely, Fermat’s Principle of Least Time. As we have considered there, Fermat’s solution is not a genuine approach of Variational Calculus. Sir Isaac Newton was the first to truly solve a problem using the techniques of Variational Calculus. The problem He considered regards finding the shape of a bow of ship having minimal resistance against a model of inbounding [fluid] particles. Newton registered his findings in His Principia, being the course of the Solution a genuine application of Variational Calculus techniques, albeit not then known as such. Being this solution of Newton the first genuine application of Variational Calculus, we are going to consider the details of this solution through the same path of reasoning took by Sir Isaac Newton – for purposes of following the evolution of ideas within this then now field of Calculus of Variations. Despite genuinely pioneering this field, Newton solved a problem that is indeed complex. Newton starts by comparing the resistance of a globe with the resistance of a cylinder, a solution that inserts the problem within the scope of Calculus, but not yet within the scope of Variational Calculus. Newton then proceeds to explore the case of a frustum of cone, entering within a scope that turned out to have a variational necessity, but not yet within the genuine scope of Variational Calculus. Then, Newton explores, using concepts of these previous structures, a genuine problem of Variational Calculus – by considering the variation of the boundary of an oval form such that the resistance against the varied boundary tend to diminish the resistance against the inbounding collisions of that model of [fluid] particles defined by Newton. Here, we are going to be limited to considering the solution Sir Isaac Newton gave to the Proposition XXXIV of His Philosophiae Naturalis Principia Mathematica.

Path to Newton’s Principia Scholium of 1685

In 1685, Sir Isaac Newton formulated a genuine problem of Variational Calculus. He also reached the solution in the same year. An edition of Newton’s Philosophiae Naturalis Principia Mathematica contains a proposition, Proposition XXXIV, stating that:

Proposition XXXIV: If in a rare medium, consisting of equal particles freely disposed at equal distances from each other, a globe and a cylinder described on equal diameters move with equal velocities in the direction of the axis of the cylinder, the resistance of the globe will be but half as great as that of the cylinder.

This proposition and its demonstration precede the Scholium to the same proposition that follows considered by Newton, being through the Scholium that Newton considers two related problems having solutions using techniques that, jointly, are proper to the scope of Variational Calculus – the first genuine implementation of Calculus of Variations to solve a problem. In the Scholium, Newton firstly considers the motion of a frustum of cone moving in the direction of its axis through that same specific medium composed of particles as defined by Newton in His Proposition XXXIV, but this first problem of the frustum becomes solved by Newton using techniques of maxima and minima – so that not then yet by an approach that is proper to Variational Calculus. Despite the fact of not being solved via Variational Calculus, the first problem considered in the Scholium has a special purpose of preceding the second problem in the Scholium, this latter problem the first one to bring techniques of Variational Calculus to appreciation. This second problem of the Scholium regards finding the shape of a solid of revolution moving through that resisting medium of particles and along the direction of its axis to satisfy the condition of minimizing the resistance against the particles of the medium.

The importance the solution Newton gave to the second problem of the Scholium, to the forthcoming epistemological evolution of the Calculus of Variations, is tremendous. The techniques used by Newton to solve the second problem of the Scholium historically propagated to the subsequent problem of Variational nature – to the Brachistochrone problem, becoming this latter problem also solved by Newton and James Bernoulli through adaptions that followed the lines of solution of the second problem in the Scholium. Euler systematized the ideas Newton used to solve the second problem of the Scholium with the adaptions that turned out to be used to solve the historically subsequent Brachistochrone problem. Sir Isaac Newton again, as a Lion, remarkably contributing. Here, we are also, as with Fermat, going to find an important characteristic from this original Newton’s contribution that will be essential along our journey – a characteristic from the considerations Newton gave in the Scholium that is related to the discontinuous nature of possible solution, which treated otherwise by means of parametric representation, would present no solution, a characteristic that will be later connected to a correspondence between Schrödinger and a colleague as we will see:

• Sir Isaac Newton has provided a Variational solution that jumps in His Scholium to Proposition XXXIV. Sir Newton works a complex scenario under the theoretical grounds of Variational Calculus and brings to the appreciation a technique of minimizing through pieces of curves, arcs, with a precluded similarity which does not preclude the Variational method of finding solution.

We are now going to analyze the solution to the problem presented by Sir Isaac Newton in His Principia, Proposition XXXIV, prior to entering the problems in the Scholium to this proposition. We are going to use a reasoning that is depicted by the Figure 1 beneath:

The Figure 1 depicts the geometry of the problem as considered by Newton in His Proposition XXXIV of His Principia. Newton considers the movement of a body through a medium that exerts a resistance on the frontal face of the body. Newton considers that the rear face of the body is not surrounded by particles – so that experiencing a region of vacuum, implying no force acts on the rear region of the immersed body. Also, Newton considers that the medium presents no friction, i.e., the force a colliding particle exerts on the body has no tangential component along the surface of the body at the collision point.

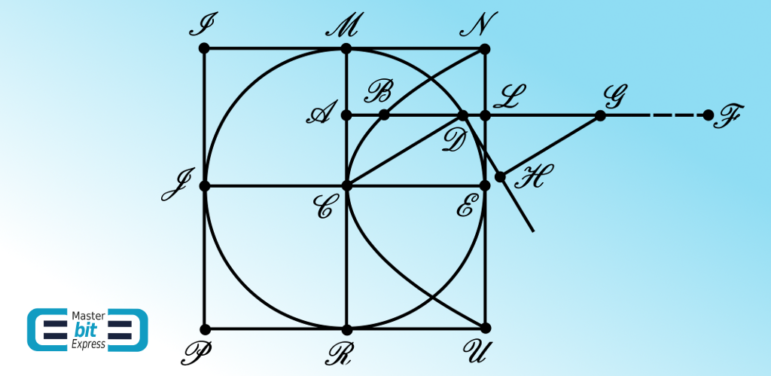
In the Figure 1, \(\mathcal{INUPI}\) is a section of cylinder and \(\mathcal{MERJM}\) is a section of sphere centered at \(\mathcal{C}\). Both the bodies are moving along the \(\mathcal{JCE}\) direction of the cylinder axis, through the medium, being this axis parallel to \(\mathcal{ADF}\). The construction of the Figure 1 is also such that the lines along \(\mathcal{CD}\) and \(\mathcal{HG}\) are perpendicular to the line along \(\mathcal{DH}\), with \(\mathcal{CD}=\mathcal{DG}\), being \(\mathcal{DH}\) tangent at \(\mathcal{D}\) to the \(\mathcal{MERJM}\) circular section. As Sir Isaac Newton points out, His Third Law allows one to equivalently consider the problem under the perspective of considering both the cylinder and the sphere at rest with the medium particles moving to the left with uniform velocity having the direction \(\mathcal{EC}\) of the cylinder’s axis. Since there will be no friction according to the collision model, a particle that hits the surface of the sphere at a point \(\mathcal{D}\) will exert a force on this point of the surface that inwards along the normal to the sphere at this collision point \([\mathcal{D}]\). The point \(\mathcal{L}\) is a point that corresponds to the point \(\mathcal{D}\), this former point \([\mathcal{L}]\) then at which there will be an inward collision on the surface of the cylinder along the direction \(\mathcal{FA}\) parallel to \(\mathcal{EC}\). According to Sir Isaac Newton, a particle of the medium that hits the sphere at the point \(\mathcal{D}\) under the angle \(\mathcal{ECD}\) in relation to the normal direction exerts a force on the sphere that is to the force the same particle perpendicularly exerts on the cylinder at the point \(\mathcal{L}\), as \(\mathcal{GH}\) is to \(\mathcal{GD}\), or \(\mathcal{DA}\) to \(\mathcal{DC}\). This proportion occurs since, by construction, \(\mathcal{CD}\,\,\parallel\,\,\mathcal{HG}\) and:
\begin{equation}
\mathcal{CD}=\mathcal{DG},\tag{1}
\end{equation}

so that, since:
\begin{eqnarray}
\mathcal{GH}&=&\mathcal{GD}\cos{\left(\mathcal{HGD}\right)}\tag{2}\\
\mathcal{AD}&=&\mathcal{CD}\cos{\left(\mathcal{ADC}\right)}\tag{3}\\
\mathcal{HGD}&=&\mathcal{ADC}\tag{4}
\end{eqnarray}

we reach:
\begin{equation}
\cos{\left(\mathcal{HGD}\right)}=\cos{\left(\mathcal{ADC}\right)}\Rightarrow\dfrac{\mathcal{GH}}{\mathcal{GD}}=\dfrac{\mathcal{AD}}{\mathcal{CD}}.\tag{5}
\end{equation}

Sir Isaac Newton calls the efficacy the force that is correspondingly exerted on the sphere, in relation to the exerted on the cylinder at point \(\mathcal{L}\), along the direction \(\mathcal{FD}\). To understand why Newton is using this qualification regarding the force, we are going to consider the force that is exerted on the sphere by an inbounding colliding particle that corresponds to the force an inbounding colliding particle moving along the direction \(\mathcal{FL}\) exerts on the cylinder at point \(\mathcal{L}\). Being \(g\) the force an inbounding colliding particle moving along \(\mathcal{FL}\) exerts on the cylinder at the collision point \(\mathcal{L}\), this force that is correspondingly exerted on the sphere along the normal direction \(\mathcal{CD}\), remembering that there is no friction, becomes \(g\cos{\mathcal{\left(ECD\right)}}=g\cos{\mathcal{\left(CDA\right)}}\). This latter force on the sphere, decomposed along the direction \(\mathcal{FD}\), becomes \(g\cos^{2}{\mathcal{\left(CDA\right)}}\). This is latter force is indeed the efficacy on the sphere, since: a decomposition that is orthogonal to \(\mathcal{FD}\) will jointly vanish by virtue of symmetry. In other words, the efficacy is the force that stands to be integrated over the considered surface.

Newton then proceeds using a technique, to reach the integration, that has a variational insight – indeed brilliant, albeit not Variational Calculus yet, which goes along a reasoning that will actually lead to the first genuine solution that indeed uses Variational Calculus in the Scholium. Newton seeks to find a way to deform a surface in relation to the effect the colliding inbounding particles exert on the cylinder, to reach the corresponding effect on the sphere. As said, His technique is intended to reach the integration. As we will see along our journey, the Variational Calculus is a mathematical field that stands for finding solutions that lead to stationary integrals. This is done, as we will see in details along our journey, by considering deformation of paths, somewhat in the sense that has been previously considered in our post on Fermat’s Variational Principle. Here, Newton is epistemologically going along a march of reasoning that has some of these ingredients prior to reaching His second solution in the Scholium to the proposition we are here dealing with. For purposes of finding this deformation to integration, Newton then seems to put the focus (as we are going to subsequently discuss) on the relation between the efficacy and the force that is originally exerted on the cylinder at the collision point \(\mathcal{L}\):
\begin{equation}
\dfrac{\text{Efficacy}}{g}=\cos^{2}{\mathcal{\left(CDA\right)}}.\tag{6}
\end{equation}

Now, let us to consider the measure:
\begin{equation}
g\propto\mathcal{LA}\Rightarrow g=\alpha\cdot\mathcal{LA}=\alpha\cdot\mathcal{CD},\tag{7}
\end{equation}

where \(\alpha\) is a convenient proportionality factor, and by the fact that \(\mathcal{LA}=\mathcal{CD}\) is the radius of the sphere. By the same token, let us to consider the measure:
\begin{equation}
\text{Efficacy}\propto\mathcal{LB}\Rightarrow\text{Efficacy}=\alpha\cdot\mathcal{LB},\tag{8}
\end{equation}

where \(\alpha\) is a convenient proportionality factor as previously defined. These measures define, by virtue of the Eqs. (6), (7) and (8):
\begin{equation}
\mathcal{LB}=\mathcal{CD}\cdot\cos^{2}{\mathcal{\left(CDA\right)}}=\mathcal{LA}\cdot\cos^{2}{\mathcal{\left(CDA\right)}}.\tag{9}
\end{equation}

Newton remarkably says: \(\mathcal{LB}\) will be to \(\mathcal{LA}\) as the effect of the particle upon the globe to the effect of the particle upon the cylinder. And therefore the solid which is formed by all the right lines \(\mathcal{LB}\) will be to the solid formed by all the right lines \(\mathcal{LA}\) as the effect of all the particles upon the globe to the effect of all the particles upon the cylinder.

This is remarkable, since, with the definition of the deformed curve \(\mathcal{NCU}\), the integration for comparing the resistance of the globe against the medium of particles with the resistance of the cylinder against the same medium of particles has been reduced to the comparison between volumes of solids, namely between the solid generated by the revolution of \(\mathcal{NC}\) and the cylinder generated by the revolution of \(\mathcal{NM}\), both around the \(\mathcal{CE}\) axis. The solid that is generated by the revolution of \(\mathcal{NC}\) around the \(\mathcal{CE}\) axis is a paraboloid and the solid generated by the revolution of \(\mathcal{NM}\) around the \(\mathcal{CE}\) axis is a cylinder (half our original cylinder) that circumscribes the paraboloid. To verify the parabolic nature of the curve \(\mathcal{NCU}\), we rewrite the Eq. (9):
\begin{eqnarray}
y&\equiv&\mathcal{LB}=\mathcal{CD}\cdot\cos{\mathcal{\left(CDA\right)}}\cdot\cos{\mathcal{\left(CDA\right)}}\nonumber\\
&=&\mathcal{DA}\cdot\dfrac{\mathcal{DA}}{\mathcal{CD}}=\dfrac{\left(\mathcal{DA}\right)^{2}}{\mathcal{CD}}=\dfrac{\left(\mathcal{CD}\right)^{2}-\left(\mathcal{CA}\right)^{2}}{\mathcal{CD}}\nonumber\\
&=&\mathcal{CD}-\dfrac{1}{\mathcal{CD}}\left(\mathcal{CA}\right)^{2}=-\dfrac{1}{\mathcal{CD}}\left(\mathcal{CA}\right)^{2}+\mathcal{CD},\tag{10}
\end{eqnarray}

which, by virtue of the radius of the sphere \(\mathcal{CD}=\mathcal{CE}\) and by defining \(\mathcal{CA}=\mathcal{EL}\equiv x\), may be rewritten to give:
\begin{equation}
y=-\dfrac{1}{\mathcal{CE}}\,x^{2}+\mathcal{CE}.\tag{11}
\end{equation}

By comparing the Eq. (11) with Figure 1, it becomes clear why the solid that is generated by the revolution of \(\mathcal{NC}\) around the \(\mathcal{CE}\) axis is a paraboloid, since \(\mathcal{NCU}\) is a parabolic curve given by the Eq. (11). Using a known result, as inferred from page 469 of The Mathematical Papers of Isaac Newton – Volume VI – Edited by D.T. Whiteside, Sir Isaac Newton states: Sed solidum prius est parabolois et solidum posterius est cylindrus circumscriptus. Et notum est quod cylindrus sit Paraboloide inscripto duplo major.

Newton is then appealing to a result firstly demonstrated by Archimedes, namely that: the volume of the frustum of a paraboloid of revolution is half that of the circumscribing cylinder. Hence, it indeed rest assured from Newton that under the circumstances defined: if the particles of the medium are at rest and the cylinder and the globe move with equal velocities, the resistance of the globe will be half the resistance of the cylinder.

Newton’s Proposition XXXIV has then been solved using geometry. Here we have finished the purpose of this post of considering this proposition prior to considering the subsequent problems of the Scholium to this proposition. As an exercise, we propose the solution of this proposition by using analysis:

• Show that the net force on an elementary arc of the curve \(\mathcal{MDE}\) is given by \(g\cos^{2}{\left(\mathcal{ADC}\right)}\,dl\), where \(dl\) is an element of arc along the curve. With an appropriate choice of axes, show that the resistance can be generically considered as being given by the following integration, and compare the resistances – by firstly obtaining the resistance of the sphere and the resistance of the cylinder:

\begin{equation}
\text{Resistance}=2\pi\int^{y_{f}}_{y_{i}}y\cos^{2}{\left(\mathcal{ADC}\right)}\,dy.\tag{12}
\end{equation}

Next post, we will consider the first problem of the Scholium – an opportunity Newton took to His masterful path to the second problem.

See You there. And all the best, indeed,

MasterBitExpress Bitcoin Wallet
Development