Dear User,

Modern Quantum Mechanics under the Schrödinger Picture has its initial roots within the Hamilton-Jacobi formulation of Analytical Mechanics. Our journey of analysis regarding the necessity of understanding in full the reduction of state in Quantum Mechanics starts by going back to the initial source of considerations regarding the characteristics of the Method that permeates Analytical Mechanics: The Variational Principle. The first considerations on the Variational Principle as a Principle of Nature under the terms of modern understanding, which includes how this principle was understood by Schrödinger, start with papers by Fermat in 1662. Here, we are going to be limited to dealing with these initial considerations of Fermat regarding two of his papers in 1662, from which not only the [variational] principle considered by Fermat is extracted as fundamental – but the role of the reference state as well.

Two Papers of Fermat

Fermat studied mathematical techniques based on conditions of extremum, viz., He has nine relevant papers on the subject of maxima and minima. Among these papers, there are two papers that were sent to a colleague in 1662 entitled: The Analysis of Refractions and The Synthesis of Refractions. The necessity of understanding an objective principle leading to the Snell-Descartes Law of Refraction is the main subject of these latter papers by Fermat.

The Snell-Descartes Law of Refraction was known by Fermat as indeed a Law of Nature regarding this phenomenon, being this knowledge based on empirical fact. The objective reality regarding why Nature behaves according to this Law of Refraction was the main objective of comprehension and analysis through these latter papers by Fermat in 1662, i.e. – the quantitative description of how Nature behaves regarding the phenomenon of refraction was not being questioned by Fermat, since Fermat knew this phenomenon as being quantitatively described by the Snell-Descartes Law of Refraction. The shut up and calculate nature of argumentation would not be sufficient to Fermat comprehension of Nature. Interesting, being the initial considerations of the Principle through which Nature behaves to lead to a phenomenon (refraction), the Variational Principle as turned out to be – and we will extensively study this Principle along our journey – done by Fermat, raising the necessity of objective comprehension regarding the phenomenon of refracion, being the kernel of the original obtention of the Schrödinger Equation by Schrödinger through a formulation of Analytical Mechanics which is a field having variational roots, Quantum Mechanics poses a difficulty that precludes objective comprehension – namely the reduction of the state in Quantum Mechanics. Despite of being, historically, epistemological starting point that makes sense to an investigation regarding the roots of the Variational Principle, namely by starting with the papers by Fermat in 1662, we reach a closed logical chain of objective necessity between origin and end regarding the matter of solving the objectivity within the reduction of state in Quantum Mechanics – a path of analysis that indeed succeeds, as we will consider through our long series of considerations, through our detailed journey.

The postulative argumentation of Fermat is that Nature has a Principle of Economic Behaviour through which: Nature behaves through the Easiest and Fastest possible ways. That two latter papers (1662) of Fermat are intended to consider this economic principle as necessary and sufficient conditions leading to the Snell-Descartes Law of Refraction. Despite being under the lens of consideration by Fermat, the Snell-Descartes Law of Refraction goes beyond this specific phenomenon of refraction of light propagating across a boundary that separates two material regions having distinct optical densities. As we will see along our journey, the Principle will be considered to solve epistemologically subsequent phenomena.

So that we have that Fermat very seems to be the first to accurately formulate and utilize this Principle of Nature. Despite having the name of Descartes on the Law of Refraction, contrary to Descartes, Fermat correctly considered the speed of light as being finite and slower in optically denser material – since Descartes considered that light should move faster in optically denser material. Furthermore, despite the consideration by Galileo of the Brachistochrone problem, Fermat seems indeed to be the first to put the kernel of the argumentation within the scope of Calculus, as said providing the accurate formulation of the underlying principle as well as its utilization under a variational argumentation as is and as was, respectively, currently understood and understood by Schrödinger. This latter assertion on Schrödinger will be considered in details along our journey even from his first personal communications regarding his then recently reached equation. We are now going to consider the first of the two papers of Fermat (1662) through which He obtains the Snell-Descartes Law of Refraction as necessary condition to the Principle of Least Time. For this purpose, we are going to use the following depicted figure, regarding the Fermat’s Analysis of Refractions paper of 1662.

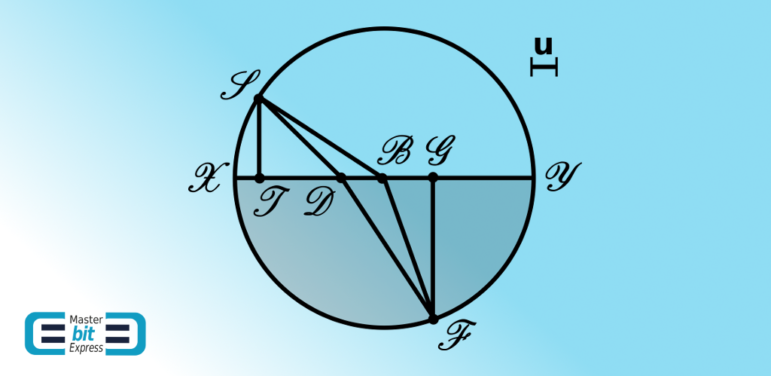
The Figure 1 depicts the geometry of the problem as considered by Fermat in one, namely Analysis of Refractions, of his two papers of 1662. This figure has a circle \(\mathcal{XSYFX}\) centered at \(\mathcal{B}\) that is composed by two optical media with distinct optical densities, \(\mathcal{XSYX}\) and \(\mathcal{YFXY}\), the latter being denser than the former. Fermat makes the assumption that a ray of light starts its propagation at point \(\mathcal{S}\) and ends at point \(\mathcal{F}\), crossing the boundary \(\mathcal{XY}\) between the two media at point \(\mathcal{D}\). Fermat encapsulates the information that the light ray encounters more difficulty to traverse the denser medium \(\mathcal{YFXY}\) than to traverse the rarer medium \(\mathcal{XSYX}\) by respectively defining the unit \(\mathcal{TB}\) as a measure of difficulty for traversing the denser medium and \(u\) as a measure of difficulty for traversing the rarer medium. There is no problem about carrying such assumptions as long as these assumptions be demonstrated as, actually, they are going to be along and from the Fermat’s march of reasoning. The concept of difficulty to a light ray to traverse a medium is considered by Fermat as being the reciprocal of the speed of the light ray across such medium. Henceforth, Fermat assumes that \(1/c_{1}\) has to be proportional to \(u\) and that \(1/c_{2}\) has to be proportional to \(\mathcal{TB}\), where \(c_{1}\) and \(c_{2}\) are respectively the speeds of the light rays through the rarer and through the denser media. Fermat, then, will have the problem of determining the point \(\mathcal{D}\) such that the light crosses the two media from point \(\mathcal{S}\) to point \(\mathcal{F}\) passing through the point \(\mathcal{D}\) at the boundary \(\mathcal{XY}\) under the condition that the traversal be accomplished taking the least, a mathematical minimum, time.

Proceeding with reasoning analogous to Fermat, we are going to use the points \(\mathcal{T}\) and \(\mathcal{G}\), which are the perpendicular projection feet from \(\mathcal{S}\) and \(\mathcal{F}\) onto the boundary \(\mathcal{XY}\), to reach the condition of minimum time, which, according to Fermat’s reasoning, reads:
\begin{equation}
\left(\mathcal{SB}\text{ in }u\right) + \left(\mathcal{SB}\text{ in }\mathcal{TB}\right).\tag{1}
\end{equation}

What does the Eq. (1) mean? Remembering that, according to Fermat’s reasoning, \(u\) is a measure of the difficulty in traversing the rarer medium \(\mathcal{XSYX}\) and that \(\mathcal{TB}\) is a measure of the difficulty in traversing the denser medium \(\mathcal{YFXY}\), Fermat is saying that when the light ray traverses the rarer medium it encounters its difficulty \(u\) and that the same ray encounters the difficulty \(\mathcal{TB}\) traversing the denser medium. The light ray connecting \(\mathcal{S}\) and \(\mathcal{B}\) becomes the light ray connecting \(\mathcal{B}\) and \(\mathcal{F}\) when this latter light ray traverses the denser medium, which is exactly what occurs and being the essence of the content of the Eq. (1), which is, under Fermat’s terms, saying that the total traverse time must be a minimum. Here, the fact that the points \(\mathcal{D}\) and \(\mathcal{B}\) are not coincident as per the depiction given by the Figure 1 is secondary, because no determination of \(\mathcal{D}\) has been yet obtained and by the fact that there will be the considered rays under reasoning according to Nature. This point of reasoning is crucial:

• There is a natural reference state dictated by measures according to Nature to vary in relation to it.

This point of reasoning is crucial and needs to be understood by a reader that is not familiar with Variational Principle. Following Fermat, this is the kernel of reasoning regarding this Principle, this is exactly the point Fermat accurately brought to appreciation. The essence of the Variational Principle will permeate all of the chain of events that followed throughout the development of Analytical Mechanics, of course with several discoveries along this chain, reaching the Hamilton-Jacobi formulation as well and the development of the Schrödinger Equation later through considerations that have root on Optics as well. We have a long journey ahead, so these considerations are just notes we are going to consider when reaching the resolution to the problem our journey is intended to solve.

Under modern reasonings, the Eq. (1) establishes that, since in a homogeneous medium the propagation time between two points separated by a distance \(L\) through the medium is:
$$
\tau_{L} = \dfrac{L}{c_{L}},\tag{2}
$$

the total time to cover the two radial distances in the distinct media of the Figure 1 is:
\begin{equation}
\text{Time}=\dfrac{\mathcal{SB}}{c_{1}} + \dfrac{\mathcal{SB}}{c_{2}}.\tag{3}
\end{equation}

Now, remembering that, as previously considered:
\begin{equation}
\alpha\,\text{Time}=\left(\mathcal{SB}\cdot u\right) + \left(\mathcal{SB}\cdot\mathcal{TB}\right),\tag{4}
\end{equation}

being the difficulty to traverse a medium proportional to the reciprocal of the velocity in the medium, being \(\alpha\) a constant of proportionality. Hence, to minimize the total time, the following quantity has to be minimized:
\begin{equation}
\left(\mathcal{SB}\cdot u\right) + \left(\mathcal{SB}\cdot\mathcal{TB}\right),\tag{5}
\end{equation}

which is that Fermat’s reasoning given by the Eq. (1).

The essence of Fermat reasoning is to ask: why does not Nature give up a little from going through \(\mathcal{B}\) by going through \(\mathcal{D}\)? Fermat is interested on an expression in terms of the quantity \(\mathcal{DB}\). Then, Fermat obtains the following expressions, which can be obtained from the Law of Cosines respectively applied to the triangles \(\mathcal{SDB}\) and \(\mathcal{FDB}\):
\begin{eqnarray}
\left(\mathcal{SD}\right)^{2}&=&\left(\mathcal{SB}\right)^{2}+\left(\mathcal{DB}\right)^{2}-2\,\mathcal{SB}\cdot\mathcal{DB}\,\cos{\left(\mathcal{DBS}\right)}\nonumber\\
&=&\left(\mathcal{SB}\right)^{2}+\left(\mathcal{DB}\right)^{2}-2\,\mathcal{DB}\cdot\mathcal{TB},\tag{6}
\end{eqnarray}

\begin{eqnarray}
\left(\mathcal{DF}\right)^{2}&=&\left(\mathcal{FB}\right)^{2}+\left(\mathcal{DB}\right)^{2}-2\,\mathcal{FB}\cdot\mathcal{DB}\,\cos{\left(\mathcal{FBD}\right)}\nonumber\\
&=&\left(\mathcal{FB}\right)^{2}+\left(\mathcal{DB}\right)^{2}+2\,\mathcal{DB}\cdot\mathcal{BG}.\tag{7}
\end{eqnarray}

Now, using the Eqs. (6) and (7), Fermat is interested on the condition to minimize the traversal time for the displaced path \(\mathcal{SDF}\):
\begin{equation}
\left(\mathcal{SD}\cdot u\right) + \left(\mathcal{DF}\cdot\mathcal{TB}\right) = \text{Minimum},\tag{8}
\end{equation}

i.e., Fermat is interested on minimize the quantity:
\begin{eqnarray}
\text{Minimum}&=&u\,\sqrt{\left(\mathcal{SB}\right)^{2}+\left(\mathcal{DB}\right)^{2}-2\,\mathcal{DB}\cdot\mathcal{TB}\,\,}\,\,+\nonumber\\
&+&\mathcal{TB}\,\sqrt{\left(\mathcal{FB}\right)^{2}+\left(\mathcal{DB}\right)^{2}+2\,\mathcal{DB}\cdot\mathcal{BG}\,\,}.\tag{9}
\end{eqnarray}

Fermat originally used a method of his own to minimize the right-hand side of the Eq. (9), his own method of maxima and minima. Of course the minimization of the Eq. (9) can be dealt with calculus, being \(\mathcal{DB}\) the independent variable. But we will propose as exercises:

• Continue to follow the Fermat reasoning, observing that the method of maxima and minima of Fermat considers that the displacement of \(\mathcal{D}\) in relation to \(\mathcal{B}\) is small, to obtain \(u=\mathcal{BG}\) and then the Snell-Descartes Law of Refraction \(\mathcal{TB}=\text{const.}\,u,\text{ where }\text{const.}>1\).
• Obtain the sufficiency, i.e., from the Snell-Descartes Law of Refraction show that one obtains the Fermat’s Variational Principle.

Fermat really seems to be the first to capture the essence of the Variational Principle by applying it to a Natural Phenomenon, but the “insertion” of Calculus was via a method of his, his method of maxima and minima. Next post, we will consider the first problem of variational nature that really starts to involve Calculus – and this was solved by a Lion: Isaac Newton.

See You there. And all the best, indeed,

MasterBitExpress Bitcoin Wallet
Development